TCEC Season 17 SuFi - Musings Online Chess

The Superfinals of the 17th season of the Top Engine Chess Championship (TCEC) has just concluded and Leela Chess Zero emerged as the champion against the mighty Stockfish with a final score of 52.5-47.5. Leela won 17 games (16 as white and 1 as black), drew 71 games, and lost 12 games (11 as black and 1 as white), to become the TCEC champion for the second time, after failing to qualify in season 16 (although it was undefeated in the Premier Division).

The breakdown of the results is shown in the table below.

Table of results

~~It shall be noted that the cutechess implementation by TCEC was not updated to properly convert Leela’s evaluation into centipawns.~~ It was actually the code for centipawn conversion that had to be updated.¹ The result was the very low centipawn evaluation scores shown by Lc0 even at more than 90% losing evaluation. This may account for the 7 losses from mates seen during the SuFi.

Below is the plot of the results of games for each engine playing as white. Note that because of contempt², SF evaluates the opening positions very conservatively as black compared to when it is playing as white. Be that as it may, the difference between Leela’s evaluation as white and SF’s evaluation as black is remarkable. Some chatters say that this could have affected SF’s performance. It has been claimed in chat that a contempt of 0 performs better against Leela. It is notable that many of the wins of Leela as white came from when its opening book evaluation was around 1 or when SF’s opening book evaluation was less than 0.5. Most notable is game 94, (Queen’s pawn game, Chigorin variation), which SF evaluated as 0.03 out of the opening book; Leela gave an evaluation of 1.18. In the reverse game that SF won as white, SF gave an evaluation of 1.55; on the other hand, Leela gave an evaluation of 1.1, which was not far from its evaluation when playing as white. While both of Leela and SF’s evaluations agree when SF was playing as white, there were some notable exceptions, specially game 7, which Leela evaluated 0.6 and Stockfish evaluated as 1.43.

Figure 1: Results as white. The x-axis corresponds to the opening book evaluation by Leela, while the y-axis corresponds to the opening book evaluation by SF. The subplot on the left shows the results with Leela playing as white. The subplot on the right shows the results with Stockfish playing as white.

There were only two games that were won as black–one by Stockfish in game 16, where Leela, playing as white, gave an opening evaluation of 0.78 and Stockfish gave an opening evaluation of 0.16; and the other one by Leela in game 95, where Stockfish, playing as white, gave an opening evaluation of 0.90 and Leela gave an opening evaluation of 0.93.

In game 16, Leela was optimistic about its position, giving evaluations \(>1\) up to move 115, slowly declining afterwards. But typical of Leela, its overzealousness to push for the win could sometimes backfire, specially during the endgame, when Leela doesn’t have enough time to analyze its position more deeply. In this case, Leela blundered the draw by moving 130 g6??.

In game 95, a French opening, Leela showed its mastery of the French, overturning a great opening advantage for white by closing the position and converting the game into the start of the only reverse wins in the entire Superfinals.

One of the more memorable moments in the Superfinals for me was game 66, when Leela’s evaluation jumped from +1.3 to +1.69 after the pawn sacrifice 25. c5!!. Leela also attempted to sacrifice another pawn on c4 afterwards on move 28 (28 ... Qxc4 does not work because 28 ... Qxc4 29. Bb3 Qb4 30. Bxf7+ Kxf7 31. Rxd6 Bg4 32.f5 gxf5 33. Bd2 Qc4 34. Qg3 Kg8 35. e5 Red8 36. Bc3 h5 37. Qe3 f4 38. Qd2 Rxd6 39. exd6 is totally winning for white) and successfully sacrificed a pawn on 29. h5 (en route to a thorn pawn?). After 29... gxh5, Stockfish’s pawn structure looked so bad.

The opening books for the Superfinals were provided by Jeroen Noomen. The distribution of ECO codes as specified in Noomen’s PGN is shown in the table below³.

ECO	Total	Openings
A	9	Startposition 1.d4; Dutch Leningrad; Budapest gambit; English 1… Nc6; Czech Benoni; Dutch; Snake Benoni; Trompovsky; Dutch
B	15	Sicilian Keres Attack; Modern Defence; Sicilian 4… Qb6; Owen’s Defence; Sicilian Dragon; Scandinavian; Caro Kann Advance; Sicilian Kan; The Black Lion; Sicilian Taimanov; Nimzowitsch Defence; Pirc Defence; Sicilian 4… Qb6; Modern Defence; Sicilian Najdorf 6.Be3
C	10	Frankenstein-Dracula gambit; French Winawer; Ruy Lopez Schliemann; Startposition 1.e4; French Classical; Fried Liver attack; French 2.d3; Ruy Lopez Zaitsev; Traxler gambit; French Advance
D	5	Slav Bronstein 5… Bg4; Benko gambit; Slav Geller gambit; QGD Chigorin; Queen’s Pawn
E	11	King’s Indian Mar del Plata; Benoni 7.Nd2; King’s Indian Sämisch; Queen’s Indian Petrosian; King’s Indian Fianchetto; King’s Indian Karpov; King’s Indian; Benoni 7.f4; King’s Indian Sämisch; Nimzo Indian; King’s Indian Mar del Plata

The table below shows the game numbers, the openings, variations, and ECO codes after transposition, the win rate (by Leela), the elo difference after each game (elodiff), the standard error of the elo differences, the likelihoods of superiority, the opening evaluations by Leela (Lc0), the opening evaluations by Stockfish (SF), and the result as white. Note that each opening is played as white by both engines in turns. SF plays each opening as white first.

game	Opening	Variation	ECO	Win Rate	elodiff	SE	LOS	Lc0	SF	Result
1	Queen's pawn game		E10	0.50	0.00		1.00	0.22	0.30	1/2-1/2
2	QGD semi-Slav		D43	0.50	0.00		1.00	0.24	-0.09	1/2-1/2
3	Sicilian	Scheveningen, Keres attack	B81	0.33	-120.41	867.95	0.93	1.35	1.22	1-0
4	Sicilian	Scheveningen, Keres attack	B81	0.50	0.00		0.84	1.36	0.92	1-0
5	King's Indian	orthodox, Aronin-Taimanov, 9.Ne1	E98	0.50	0.00	798.10	0.89	0.59	0.48	1/2-1/2
6	King's Indian	orthodox, Aronin-Taimanov, 9.Ne1	E98	0.50	0.00	472.71	0.93	0.63	0.00	1/2-1/2
7	Vienna game		C27	0.43	-49.98	318.79	0.88	0.60	1.43	1-0
8	Vienna	`Frankenstein-Dracula' variation	C27	0.44	-43.66	289.95	0.91	0.73	0.69	1/2-1/2
9	Dutch defence		A81	0.44	-38.76	267.65	0.93	0.81	0.89	1/2-1/2
10	Dutch defence		A81	0.45	-34.86	249.73	0.95	0.84	0.49	1/2-1/2
11	French	Winawer, advance variation	C16	0.45	-31.67	234.94	0.97	0.84	0.67	1/2-1/2
12	French	Winawer, advance variation	C16	0.50	0.00	235.95	0.93	1.09	0.30	1-0
13	Benoni	Nimzovich (knight's tour) variation	A61	0.50	0.00	222.81	0.95	0.72	0.77	1/2-1/2
14	Benoni	Nimzovich (knight's tour) variation	A61	0.54	24.86	223.46	0.92	0.73	0.60	1-0
15	Robatsch (modern) defence		B06	0.53	23.20	211.89	0.93	0.59	0.68	1/2-1/2
16	Robatsch (modern) defence		B06	0.50	0.00	193.67	0.91	0.78	0.16	0-1
17	Budapest defence		A52	0.50	0.00	186.24	0.92	0.72	0.55	1/2-1/2
18	Budapest defence		A52	0.50	0.00	179.62	0.93	0.74	0.30	1/2-1/2
19	Sicilian defence		B32	0.50	0.00	173.65	0.94	0.67	0.82	1/2-1/2
20	Sicilian defence		B32	0.50	0.00	168.25	0.95	0.73	0.41	1/2-1/2
21	King's Indian	Saemisch, Panno main line	E84	0.50	0.00	163.32	0.96	0.47	0.42	1/2-1/2
22	King's Indian	Saemisch, Panno main line	E84	0.50	0.00	158.80	0.97	0.65	0.00	1/2-1/2
23	Ruy Lopez	Schliemann defence, Berger variation	C63	0.50	0.00	154.64	0.97	0.76	1.21	1/2-1/2
24	Ruy Lopez	Schliemann defence, Berger variation	C63	0.50	0.00	150.80	0.98	0.77	0.83	1/2-1/2
25	QGD Slav	Steiner variation	D16	0.50	0.00	147.22	0.98	1.24	1.22	1/2-1/2
26	QGD Slav	Steiner variation	D16	0.52	13.37	146.49	0.97	1.30	1.07	1-0
27	Owen defence		B00	0.50	0.00	140.78	0.95	0.99	0.83	1-0
28	Owen defence		B00	0.52	12.41	140.05	0.94	1.00	0.44	1-0
29	Queen's Indian	Petrosian system	E12	0.50	0.00	135.11	0.93	0.90	1.00	1-0
30	Queen's Indian	Petrosian system	E12	0.50	0.00	132.53	0.93	0.88	0.47	1/2-1/2
31	Ruy Lopez	Berlin defence	C65	0.50	0.00	130.08	0.94	0.21	0.62	1/2-1/2
32	Sicilian	Najdorf, Opovcensky variation	B92	0.50	0.00	127.77	0.95	0.37	0.00	1/2-1/2
33	King's Indian	fianchetto, classical main line	E69	0.48	-10.53	124.22	0.93	0.93	0.93	1-0
34	King's Indian	fianchetto, classical main line	E69	0.50	0.00	123.49	0.92	0.92	0.20	1-0
35	Sicilian	dragon, Yugoslav attack, 9.Bc4	B77	0.50	0.00	121.51	0.93	0.91	1.00	1/2-1/2
36	Sicilian	dragon, Yugoslav attack, 12.h4	B79	0.51	9.65	120.87	0.92	0.95	0.80	1-0
37	English opening		A10	0.51	9.39	118.99	0.92	0.61	0.62	1/2-1/2
38	English opening		A10	0.53	18.30	118.42	0.91	0.63	0.27	1-0
39	French	Steinitz, Boleslavsky variation	C11	0.53	17.83	116.64	0.92	0.49	0.48	1/2-1/2
40	French	Steinitz, Boleslavsky variation	C11	0.53	17.39	114.94	0.92	0.50	0.17	1/2-1/2
41	Semi-Benoni (`blockade variation')		A44	0.52	16.96	113.31	0.93	1.49	1.31	1/2-1/2
42	Semi-Benoni (`blockade variation')		A44	0.52	16.56	111.75	0.93	1.48	1.00	1/2-1/2
43	Scandinavian	Pytel-Wade variation	B01	0.51	8.08	109.32	0.92	1.03	0.98	1-0
44	Scandinavian	Pytel-Wade variation	B01	0.52	15.80	108.81	0.92	1.03	0.85	1-0
45	Benko gambit		A57	0.52	15.45	107.43	0.92	0.52	0.54	1/2-1/2
46	Benko gambit		A57	0.52	15.12	106.10	0.92	0.55	0.00	1/2-1/2
47	Caro-Kann	advance variation	B12	0.52	14.79	104.81	0.93	0.03	0.00	1/2-1/2
48	Caro-Kann	advance variation	B12	0.52	14.48	103.58	0.93	0.03	0.00	1/2-1/2
49	King's Indian	Makagonov system (5.h3)	E71	0.52	14.19	102.38	0.94	-0.67	0.48	1/2-1/2
50	King's Indian	Makagonov system (5.h3)	E71	0.52	13.90	101.23	0.94	-0.66	0.17	1/2-1/2
51	Sicilian	Kan, 5.Bd3	B42	0.52	13.63	100.12	0.94	0.67	0.62	1/2-1/2
52	Sicilian	Kan, 5.Bd3	B42	0.52	13.37	99.04	0.95	0.69	0.23	1/2-1/2
53	Dutch defence, Blackburne variation		A81	0.52	13.12	98.00	0.95	0.58	0.75	1/2-1/2
54	Dutch defence, Blackburne variation		A81	0.52	12.87	96.99	0.95	0.59	0.42	1/2-1/2
55	Pirc defence		B07	0.52	12.64	96.01	0.96	0.71	0.86	1/2-1/2
56	Pirc defence		B07	0.52	12.41	95.06	0.96	0.71	0.55	1/2-1/2
57	Benoni defence		A60	0.52	12.20	94.14	0.96	1.05	0.99	1/2-1/2
58	Benoni defence		A60	0.52	11.99	93.24	0.97	1.05	0.58	1/2-1/2
59	two knights defence	Fegatello attack	C57	0.52	11.78	92.37	0.97	0.49	0.80	1/2-1/2
60	two knights defence	Fegatello attack	C57	0.52	11.59	91.52	0.97	0.49	0.46	1/2-1/2
61	Trompovsky attack (Ruth, Opovcensky opening)		A45	0.52	11.40	90.70	0.97	0.48	0.61	1/2-1/2
62	Trompovsky attack (Ruth, Opovcensky opening)		A45	0.52	11.21	89.90	0.97	0.49	0.00	1/2-1/2
63	Reti	King's Indian attack, French variation	A08	0.52	11.03	89.12	0.98	-0.15	0.00	1/2-1/2
64	Reti	King's Indian attack, French variation	A08	0.52	10.86	88.36	0.98	-0.12	-0.52	1/2-1/2
65	King's Indian	4.e4	E70	0.52	10.69	87.62	0.98	0.67	0.82	1/2-1/2
66	King's Indian	orthodox variation	E94	0.52	15.80	87.29	0.97	0.71	0.09	1-0
67	Sicilian	Taimanov (Bastrikov) variation	B47	0.52	15.57	86.57	0.98	-0.85	0.05	1/2-1/2
68	Sicilian	Taimanov (Bastrikov) variation	B47	0.52	15.34	85.87	0.98	-0.79	0.00	1/2-1/2
69	QGD Slav	Slav gambit	D15	0.52	15.12	85.19	0.98	-0.06	0.00	1/2-1/2
70	QGD Slav	Slav gambit	D15	0.52	14.90	84.52	0.98	-0.03	-0.43	1/2-1/2
71	KP	Nimzovich defence	B00	0.52	14.69	83.87	0.98	0.42	0.35	1/2-1/2
72	KP	Nimzovich defence	B00	0.52	14.48	83.23	0.98	0.44	0.03	1/2-1/2
73	Benoni	Taimanov variation	A67	0.52	14.29	82.61	0.98	0.78	0.93	1/2-1/2
74	Benoni	Taimanov variation	A67	0.52	14.09	82.01	0.99	0.79	0.34	1/2-1/2
75	Pirc defence		B07	0.52	13.90	81.41	0.99	0.67	0.70	1/2-1/2
76	Pirc defence		B07	0.52	13.72	80.83	0.99	0.67	0.45	1/2-1/2
77	QGD	Chigorin defence	D07	0.51	9.03	79.98	0.98	0.76	1.21	1-0
78	QGD	Chigorin defence	D07	0.51	8.91	79.43	0.98	0.78	0.72	1/2-1/2
79	Ruy Lopez	closed, Flohr-Zaitsev system (Lenzerheide variation)	C92	0.51	8.80	78.89	0.99	0.56	0.46	1/2-1/2
80	Ruy Lopez	closed, Flohr-Zaitsev system (Lenzerheide variation)	C92	0.51	8.69	78.37	0.99	0.58	0.13	1/2-1/2
81	King's Indian	Saemisch, orthodox, Bronstein variation	E87	0.51	8.58	77.85	0.99	0.45	1.23	1/2-1/2
82	King's Indian	Saemisch, orthodox, Bronstein variation	E87	0.51	8.48	77.34	0.99	0.55	0.19	1/2-1/2
83	Sicilian defence		B40	0.51	4.19	76.62	0.99	1.02	1.08	1-0
84	Sicilian defence		B40	0.51	8.27	76.36	0.98	1.04	0.67	1-0
85	Dutch		A80	0.51	8.18	75.88	0.98	0.74	0.86	1/2-1/2
86	Dutch		A80	0.51	8.08	75.41	0.98	0.76	0.37	1/2-1/2
87	King's Indian	orthodox, Donner variation	E94	0.51	3.99	74.75	0.98	0.90	0.59	1-0
88	Robatsch (modern) defence		B06	0.51	7.90	74.50	0.98	0.97	0.50	1-0
89	Nimzo-Indian	4.e3 O-O, 5.Bd3	E47	0.51	7.81	74.05	0.98	0.28	0.00	1/2-1/2
90	Nimzo-Indian	4.e3 O-O, 5.Bd3	E47	0.51	7.72	73.62	0.98	0.33	-0.12	1/2-1/2
91	two knights defence	Wilkes Barre (Traxler) variation	C57	0.51	7.64	73.19	0.98	1.40	1.46	1/2-1/2
92	two knights defence	Wilkes Barre (Traxler) variation	C57	0.52	11.33	72.96	0.98	1.40	1.01	1-0
93	Queen's pawn game, Chigorin variation		D02	0.51	7.47	72.35	0.97	1.10	1.55	1-0
94	Queen's pawn game, Chigorin variation		D02	0.52	11.09	72.13	0.97	1.18	0.03	1-0
95	French	advance variation	C02	0.52	14.64	71.91	0.97	0.93	0.90	0-1
96	French	advance variation	C02	0.53	18.11	71.70	0.96	0.97	0.28	1-0
97	King's Indian	orthodox, Aronin-Taimanov, 9.Ne1	E98	0.53	17.92	71.30	0.96	0.43	0.47	1/2-1/2
98	King's Indian	orthodox, Aronin-Taimanov, 9.Ne1	E98	0.53	21.30	71.10	0.96	0.49	0.00	1-0
99	Sicilian	Najdorf, Byrne (English) attack	B90	0.53	17.56	70.52	0.96	0.78	1.01	1-0
100	Sicilian	Najdorf, Byrne (English) attack	B90	0.53	17.39	70.15	0.96	0.82	0.14	1/2-1/2

We see that elo difference after 100 games is around 17 but with large error bars (SE=70.15). I wonder how the elo difference will play out with larger sample size.

We can now see the estimated ELO differences at the last of game of each ECO group of openings.

ECO2	Score.Leela	Score.SF	total	draw_ratio	wins.Leela	losses.Leela	wins.SF	losses.SF	Draws	win_rate.Leela	elodiff	SE	LOS
A	13.0	11.0	24	0.91667	2	0	0	2	22	0.54167	29.020	157.50	1.00000
B	15.0	15.0	30	0.60000	6	6	6	6	18	0.50000	0.000	132.53	0.89435
C	10.0	7.0	17	0.70588	4	1	1	4	12	0.58824	61.961	212.74	0.95543
D	4.5	4.5	9	0.55556	2	2	2	2	5	0.50000	0.000	296.58	0.86971
E	10.0	10.0	20	0.70000	3	3	3	3	14	0.50000	0.000	168.25	0.95221

We see that Leela racked up the lead through the A and C openings in this season.

Looking at the opening evaluations by ECO family of codes, we can see that the opening evaluations do not differ when Stockfish played white and Leela played black. But the opening evaluations differed a lot when SF played black and Leela played white. Notice though that D openings were evaluated almost similarly by Stockfish and Leela.

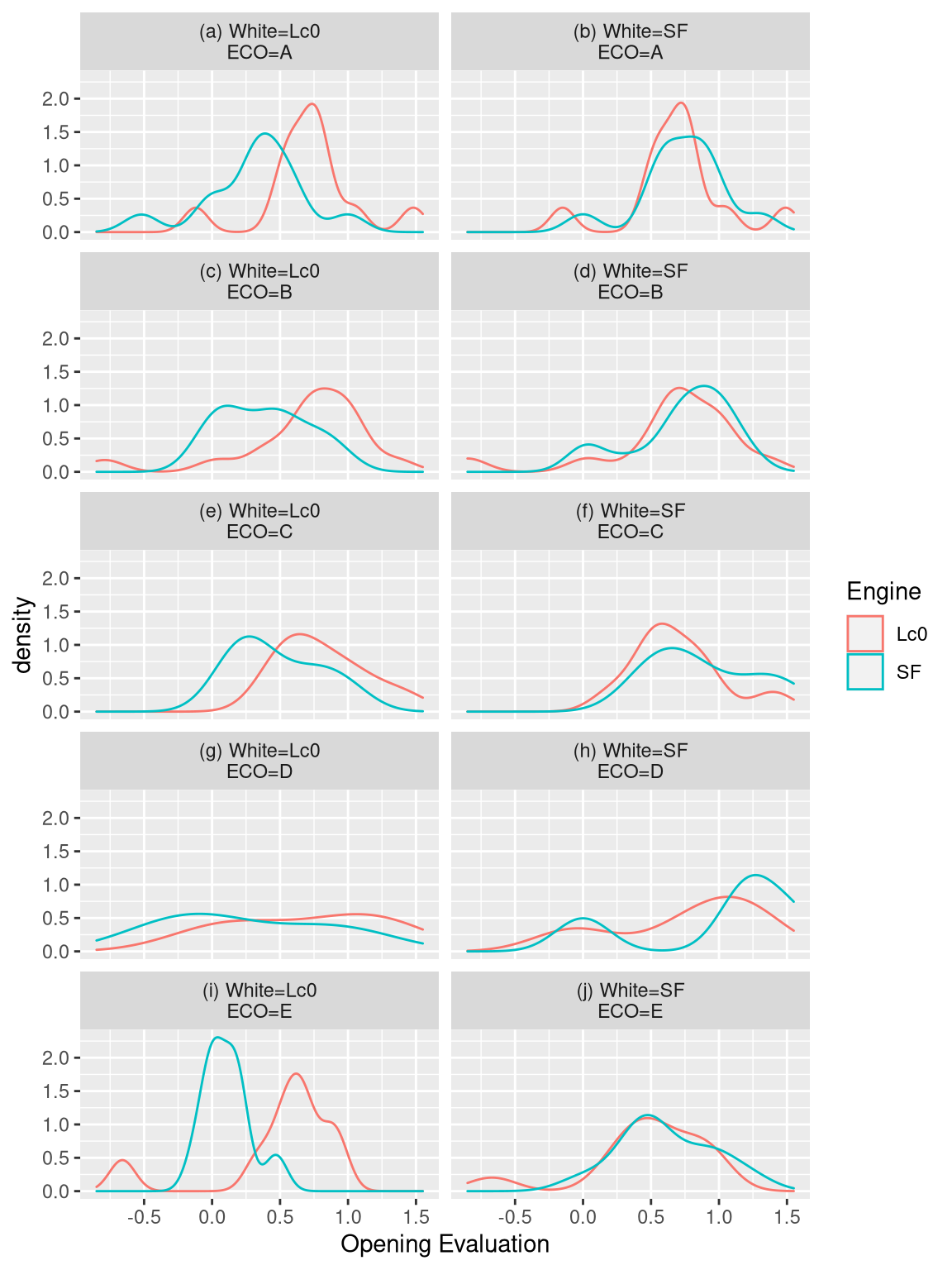
Figure 2: Distribution of opening evaluations for different ECO codes

Quite interesting too is the number of moves in each game (mean =101.92, sd =46.79). Games were considerably quite shorter if Stockfish was playing white (mean =87.2, sd =40.13), specially when it was winning (mean = 68.09, sd = 19.44). Games took a while to finish when Leela was playing white (mean = 116.64, sd = 48.69), specially when it was winning (mean = 124.12, sd = 41.55). However, SF lost as white (game 95, 93 moves) in much shorter time than it did winning as black (game 16, 196 moves, coming via a long series of high level shuffling from a fortress-y position, after Leela pressed for activity as discussed above).

Figure 3: Distribution of number of moves based on results and each engine playing as white.

We also see that for this SuFi, the rooks and the king moved the most, perhaps due to many pawn and rook endings.

Figure 4: Distribution of number of moves by piece

Finally, Leela’s evaluations seemed to agree with SF’s evaluation up to a certain centipawn value only, around \((-3,3)\). ~~The reason was that TCEC had yet to update the system to reflect correct centipawn evaluation.~~ (Again, it was the Leela centipawn code that had to be updated.) This resulted in a lot of mates during the competition. Here is an attempt to model Leela’s centipawn evaluation based on SF’s evaluation. I have stored the matched evaluations throughout the games here. This CSV file contains all of the evaluations in all games for which Leela’s evaluation is in \((-4,4)\) and Stockfish’s evaluation is in \((-20,20)\). The reason for the choice of limits is nothing special–one engine evaluation seem to be well-behaved with respect to the other engine evaluation. I have also removed the last move of the engine with the greater number of moves so that the number of evaluations will match.

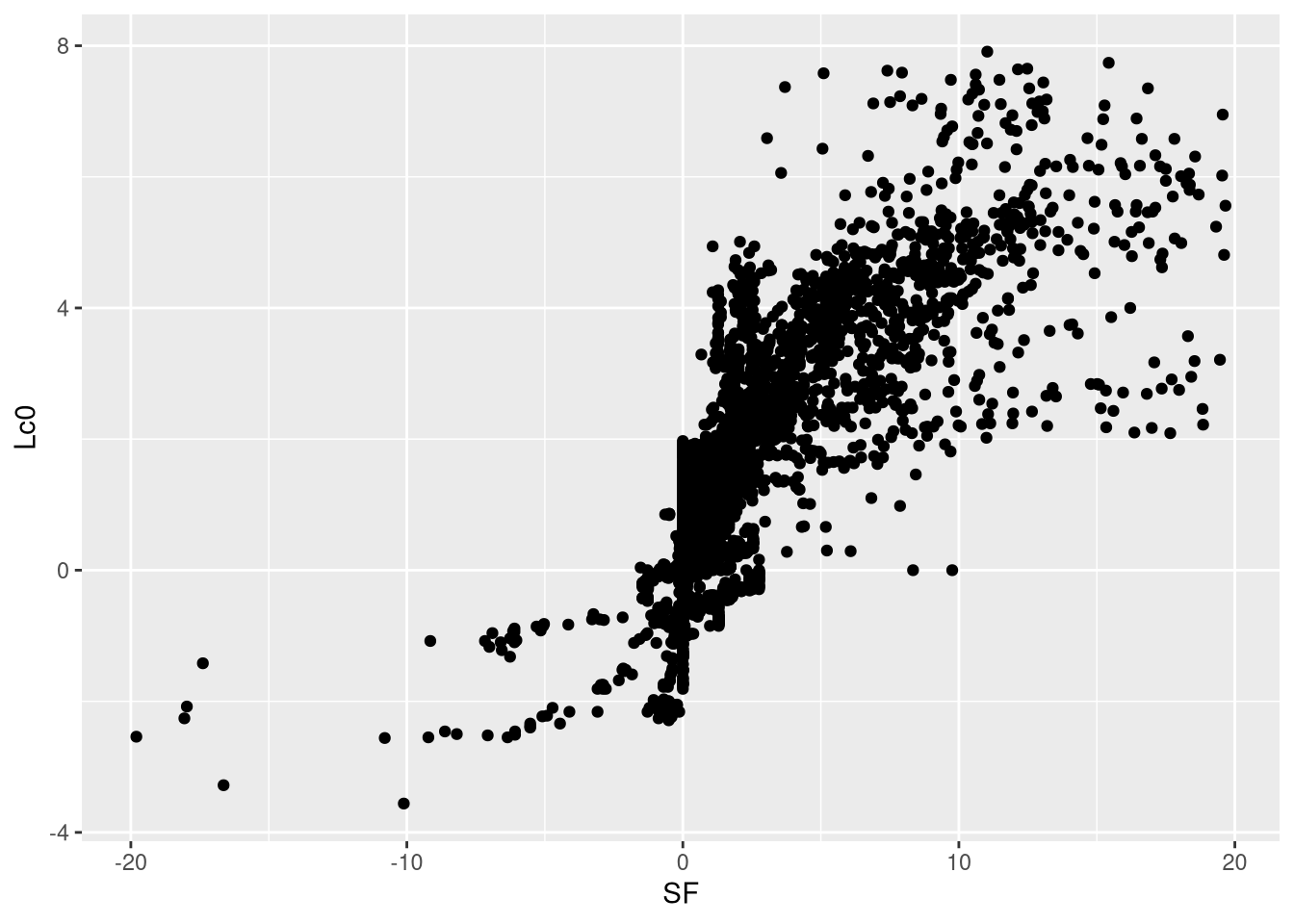
Figure 5: Plot of Leela’s evaluations against Stockfish’s evaluations

I fitted a logistic curve to the evaluations. To do this, I added 20 to SF’s evals and 4 to Leela’s evals and proceeded to fit the model in R.

evals_comp <- read.csv("evals_tcec.csv")

x <- evals_comp$SF + 20
y <- evals_comp$Lc0 + 4
data.df <- data.frame(x=x, y=y)
max(y)

## [1] 11.91

logit <- qlogis
model.0 <- lm(logit(y/12) ~ x, data=data.df) 
summary(model.0)

## 
## Call:
## lm(formula = logit(y/12) ~ x, data = data.df)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.271 -0.154 -0.028  0.173  3.747 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -3.64397    0.02670    -136   <2e-16 ***
## x            0.15413    0.00125     124   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.334 on 8976 degrees of freedom
## Multiple R-squared:  0.63,   Adjusted R-squared:  0.63 
## F-statistic: 1.53e+04 on 1 and 8976 DF,  p-value: <2e-16

phi1 <- 12
phi2 <- coef(model.0)[1]
phi3 <- coef(model.0)[2]
model<-nls(y~phi1/(1+exp(-(phi2+phi3*x))),
 start=list(phi1=phi1,phi2=phi2,phi3=phi3),data=data.df,trace=TRUE)

## 6218.7 :  12.00000 -3.64397  0.15413
## 5969.8 :  10.50614 -4.03318  0.18298
## 5779.1 :   9.16663 -4.92558  0.23813
## 5325.2 :   8.8094 -6.4689  0.3196
## 5287.8 :   8.97024 -6.74805  0.33167
## 5287.8 :   8.95998 -6.77621  0.33319
## 5287.8 :   8.95897 -6.77960  0.33337
## 5287.8 :   8.95885 -6.77999  0.33339

summary(model)

## 
## Formula: y ~ phi1/(1 + exp(-(phi2 + phi3 * x)))
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## phi1  8.95885    0.04817   186.0   <2e-16 ***
## phi2 -6.77999    0.10502   -64.6   <2e-16 ***
## phi3  0.33339    0.00552    60.4   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.768 on 8975 degrees of freedom
## 
## Number of iterations to convergence: 7 
## Achieved convergence tolerance: 4.68e-06

#set parameters
phi1<-coef(model)[1]
phi2<-coef(model)[2]
phi3<-coef(model)[3]
x<-c(min(data.df$x):max(data.df$x)) #construct a range of x values bounded by the data
y<-phi1/(1+exp(-(phi2+phi3*(x)))) #predicted SF's evals
predict<-data.frame(x=x-20,y=y-4) #create the prediction data frame

# create a plot of actual values and the predictions from fitted model
ggplot(data=evals_comp,aes(x=SF,y=Lc0))+
geom_point(size=1)+theme_bw()+
labs(x='SF',y='Lc0')+
geom_line(data=predict,aes(x=x,y=y), size=1, color = "blue")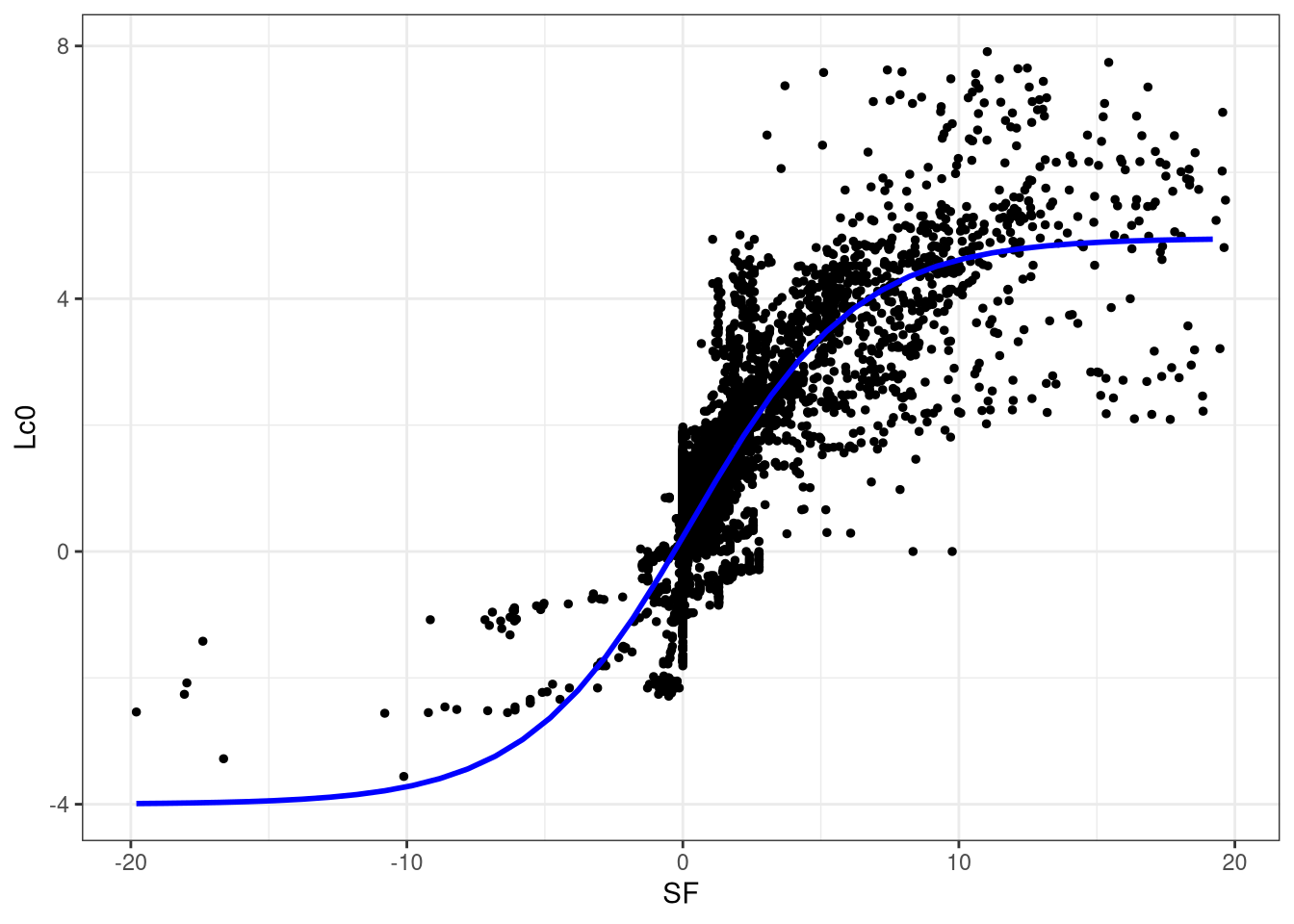

Figure 6: Logistic fit over Leela and Stockfish’s evaluations.

Update: 24 April 2020

Playing Times

All of the SuFi games went on for a total duration of 12.88115 days (except for short intervals between games). The average time for a SuFi game is 03:05 with a standard deviation of 00:29.

The following table shows some summary statistics by ECO code for the whole SuFi.

ECO	Duration	SD	Min	Q1	Median	Q3	Max
A	03:08:47	00:28:18	01:49:21	03:02:38	03:15:22	03:25:06	03:47:33
B	03:09:01	00:28:32	01:47:40	03:05:55	03:15:26	03:25:46	03:43:47
C	03:09:03	00:23:25	01:59:41	02:56:31	03:16:57	03:25:45	03:33:36
D	02:51:02	00:44:50	01:48:25	01:59:55	03:06:28	03:34:50	03:35:08
E	02:59:43	00:29:38	01:53:13	02:54:02	03:06:54	03:19:40	03:33:49

The following table shows some summary statistics by ECO code with Leela playing white.

ECO	Duration	SD	Min	Q1	Median	Q3	Max
A	03:10:06	00:35:01	01:49:21	03:13:04	03:18:08	03:27:09	03:47:33
B	03:21:19	00:17:23	02:29:48	03:15:29	03:21:20	03:33:58	03:43:47
C	03:13:38	00:16:15	02:52:53	02:57:20	03:17:01	03:26:29	03:33:36
D	02:54:39	00:55:22	01:48:25	01:59:55	03:34:50	03:34:58	03:35:08
E	03:07:35	00:30:05	01:53:13	03:07:59	03:16:38	03:22:43	03:30:48

The following table shows some summary statistics by ECO code with Stockfish playing white.

ECO	Duration	SD	Min	Q1	Median	Q3	Max
A	03:07:28	00:21:03	02:34:48	02:54:04	03:13:34	03:21:52	03:37:21
B	02:54:58	00:32:41	01:47:40	02:37:32	03:06:51	03:14:52	03:37:20
C	03:04:59	00:28:44	01:59:41	02:55:55	03:16:57	03:22:34	03:27:18
D	02:46:30	00:34:57	01:55:14	02:38:54	02:59:58	03:07:33	03:10:48
E	02:53:16	00:29:03	01:57:29	02:39:00	02:58:18	03:07:52	03:33:49

Which engine is a better predictor of wins?

Alexander Lyashuk (crem), one of Leela’s lead developers, pointed me to a plot that he made that shows how the opening evaluations predict the outcome of each opening. Here is my take with scatter plots. Overall, Leela is a better predictor of 1-0 wins, specially when playing as white.

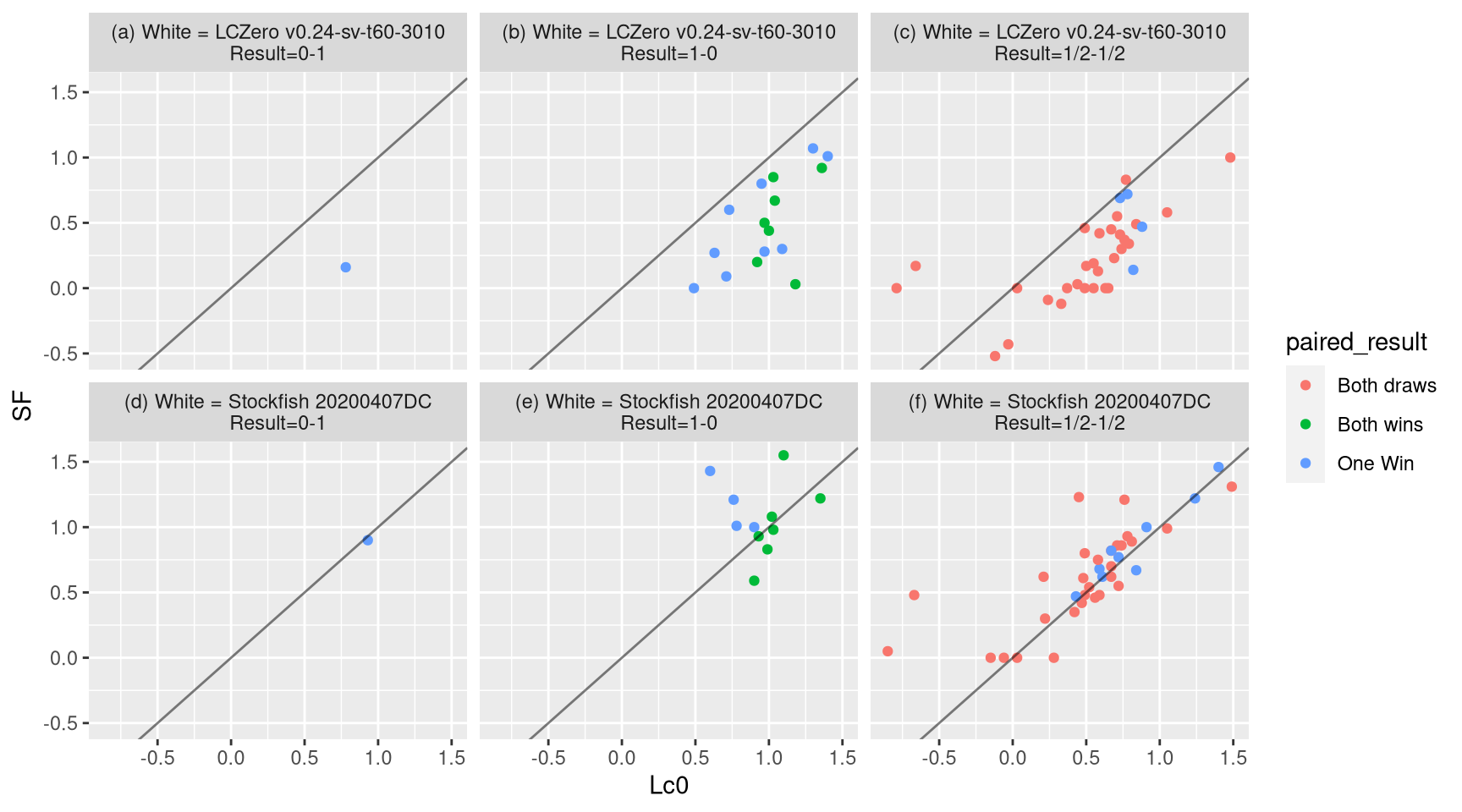
Figure 7: Outcome based on opening engine evaluations

https://github.com/LeelaChessZero/lc0/pull/1193 ↩︎
SF submitted a special binary that is supposed to have a contempt of 24 when playing as white, and a contempt of 0 when playing as black (DC=double contempt in the TCEC label for Stockfish). However, the settings were “misfixed” since with black the contempt \(c=0\) applies only to the first three moves in every iteration, but not after; hence, the contempt is effectively \(c=24\).↩︎
http://blogchess2016.blogspot.com/2020/03/opening-selection-tcec-17-superfinal.html ↩︎