An attempt at analyzing the TCEC Season 15 SuFi openings

My aim here is to try to analyze and make sense of what happened in the TCEC Seasono 15 SuFi, based on the ECO group of openings. Based on Jeroen Noomen’s blog, the following are the intended openings:

ECO code distribution
ECO A: 15 lines
ECO B: 14 lines
ECO C: 11 lines
ECO D: 3 lines
ECO E: 7 lines

However, the ECO code distribution may have changed because of some transpositions. I have stored the results of the TCEC Season 15 SuFi here.

library(tidyverse)
library(elo)
library(flextable)
library(officer)
data <- read_delim("./leelasf2.csv", delim = ";")
data %>% flextable() %>% autofit()

Opening	White	Black	points.White	points.Black	ECO1	plies	Leela.openeval	SF.openeval
1	SF	Leela	0.5	0.5	E73	13	0.79	1.01
2	Leela	SF	0.5	0.5	E73	13	1.28	0.43
3	SF	Leela	0.5	0.5	B84	30	0.42	0.72
4	Leela	SF	0.5	0.5	B84	30	0.43	0.32
5	SF	Leela	0.5	0.5	A80	3	0.81	0.56
6	Leela	SF	0.5	0.5	A80	3	0.84	0.24
7	SF	Leela	0.5	0.5	C37	8	-1.16	-0.36
8	Leela	SF	0.5	0.5	C37	8	-1.06	-1.05
9	SF	Leela	0.5	0.5	A60	6	1.20	0.83
10	Leela	SF	1.0	0.0	A67	6	1.17	0.34
11	SF	Leela	0.5	0.5	C05	17	0.35	0.52
12	Leela	SF	0.0	1.0	C05	17	0.38	0.09
13	SF	Leela	0.5	0.5	A30	22	0.58	0.95
14	Leela	SF	0.5	0.5	A30	22	0.72	0.36
15	SF	Leela	0.5	0.5	B06	8	1.30	1.01
16	Leela	SF	1.0	0.0	B06	8	1.38	0.61
17	SF	Leela	0.5	0.5	E97	22	1.10	1.43
18	Leela	SF	1.0	0.0	E97	22	1.57	0.72
19	SF	Leela	0.5	0.5	B69	13	0.66	0.62
20	Leela	SF	0.5	0.5	B69	13	0.68	0.19
21	SF	Leela	0.5	0.5	D31	14	0.66	0.53
22	Leela	SF	0.5	0.5	D31	14	0.70	0.00
23	SF	Leela	0.5	0.5	C92	24	0.91	0.98
24	Leela	SF	1.0	0.0	C92	24	1.10	0.21
25	SF	Leela	0.5	0.5	E15	21	0.88	0.73
26	Leela	SF	1.0	0.0	E15	21	0.90	0.32
27	SF	Leela	0.5	0.5	B01	4	1.10	0.75
28	Leela	SF	0.5	0.5	B01	4	1.13	0.42
29	SF	Leela	0.5	0.5	A50	4	0.95	0.66
30	Leela	SF	0.5	0.5	A50	4	0.98	0.33
31	SF	Leela	0.5	0.5	C52	17	-0.30	0.00
32	Leela	SF	0.5	0.5	C52	17	-0.31	-0.61
33	SF	Leela	0.5	0.5	E83	12	0.73	0.74
34	Leela	SF	0.5	0.5	E84	12	0.79	0.24
35	SF	Leela	1.0	0.0	B90	22	0.99	0.79
36	Leela	SF	1.0	0.0	B90	22	1.00	0.32
37	SF	Leela	0.5	0.5	A21	16	0.73	0.68
38	Leela	SF	1.0	0.0	A21	16	0.75	0.00
39	SF	Leela	1.0	0.0	C19	16	1.41	0.96
40	Leela	SF	1.0	0.0	C19	16	1.50	0.57
41	SF	Leela	0.5	0.5	E94	8	1.15	0.80
42	Leela	SF	0.5	0.5	A55	8	1.18	0.66
43	SF	Leela	1.0	0.0	C57	10	1.37	0.80
44	Leela	SF	0.5	0.5	C57	10	1.42	0.65
45	SF	Leela	1.0	0.0	A50	6	0.83	0.68
46	Leela	SF	0.5	0.5	A50	6	0.84	0.41
47	SF	Leela	0.5	0.5	B12	16	0.55	0.75
48	Leela	SF	0.5	0.5	B12	16	0.62	0.00
49	SF	Leela	0.5	0.5	E92	17	0.84	0.97
50	Leela	SF	0.5	0.5	E92	17	0.86	0.27
51	SF	Leela	0.5	0.5	B21	15	-0.86	-0.64
52	Leela	SF	0.5	0.5	B21	15	-0.78	-0.94
53	SF	Leela	0.5	0.5	A92	10	0.99	0.86
54	Leela	SF	0.5	0.5	A92	10	1.02	0.52
55	SF	Leela	0.5	0.5	B06	6	1.25	0.92
56	Leela	SF	0.5	0.5	B06	6	1.27	0.50
57	SF	Leela	0.5	0.5	A77	22	1.13	1.14
58	Leela	SF	0.5	0.5	A77	22	1.11	0.49
59	SF	Leela	0.5	0.5	C21	9	-1.21	-0.27
60	Leela	SF	0.5	0.5	C21	9	-0.64	-0.76
61	SF	Leela	0.0	1.0	A45	13	0.74	0.95
62	Leela	SF	1.0	0.0	A45	13	0.83	0.28
63	SF	Leela	0.5	0.5	C03	15	0.72	0.54
64	Leela	SF	0.5	0.5	C03	15	0.68	0.16
65	SF	Leela	0.5	0.5	E71	13	0.71	0.79
66	Leela	SF	0.5	0.5	E71	13	0.71	0.37
67	SF	Leela	0.5	0.5	B48	18	0.83	0.82
68	Leela	SF	0.5	0.5	B48	18	0.96	0.28
69	SF	Leela	0.5	0.5	D43	24	0.54	0.49
70	Leela	SF	0.5	0.5	D43	24	0.57	0.00
71	SF	Leela	0.5	0.5	C25	6	-0.76	0.00
72	Leela	SF	0.5	0.5	C25	6	-0.77	-0.81
73	SF	Leela	0.5	0.5	A59	12	1.51	1.00
74	Leela	SF	0.5	0.5	A58	12	1.53	0.52
75	SF	Leela	0.5	0.5	B07	9	0.77	0.77
76	Leela	SF	0.5	0.5	B07	9	1.10	0.32
77	SF	Leela	0.5	0.5	C50	0	0.34	0.62
78	Leela	SF	0.5	0.5	E06	0	0.37	0.00
79	SF	Leela	0.5	0.5	C75	10	0.76	0.76
80	Leela	SF	0.5	0.5	C75	10	0.77	0.30
81	SF	Leela	1.0	0.0	E87	12	0.99	0.81
82	Leela	SF	1.0	0.0	E88	12	1.04	0.51
83	SF	Leela	0.5	0.5	B76	28	0.67	0.58
84	Leela	SF	0.5	0.5	B76	28	1.18	0.38
85	SF	Leela	0.5	0.5	A89	14	1.58	0.94
86	Leela	SF	1.0	0.0	A89	14	1.60	0.42
87	SF	Leela	1.0	0.0	A42	6	0.82	0.69
88	Leela	SF	1.0	0.0	E94	6	0.85	0.17
89	SF	Leela	0.5	0.5	A61	19	1.25	0.97
90	Leela	SF	0.5	0.5	A61	19	1.16	0.48
91	SF	Leela	0.5	0.5	C33	7	-1.01	-0.22
92	Leela	SF	0.5	0.5	C33	7	-0.94	-0.94
93	SF	Leela	0.5	0.5	D02	4	0.96	0.74
94	Leela	SF	1.0	0.0	D02	4	0.98	0.39
95	SF	Leela	0.5	0.5	C13	11	0.64	0.51
96	Leela	SF	0.5	0.5	C13	11	0.61	0.00
97	SF	Leela	0.5	0.5	E98	20	0.55	1.16
98	Leela	SF	0.5	0.5	E98	20	0.58	0.56
99	SF	Leela	0.5	0.5	B45	14	1.17	0.96
100	Leela	SF	0.5	0.5	B45	14	1.54	0.50

First, let’s estimate the ELO differences between Leela and Stockfish after every game. Initially, the estimated ELO’s are 3589 for Leela and 3587 for Stockfish.

Let \(R_A\) be the ELO of engine \(A\) and \(R_B\) be the rating of engine \(B\). Then the expected result for engine A against B is given by the logistic equation:

\[\begin{equation} E_A = \frac{1}{1+10^{(R_A-R_B)/400}}. \end{equation}\]

Solving this equation for \(R_A-R_B\), we have:

\[\begin{equation} elodiff = R_A-R_B = 400\log_{10}\left( \frac{1-E_A}{E_A}\right) \end{equation}\]

Here we note that \((1-E_A)/E_A\) can be expressed as win ratio / loss ratio without loss of generality. That is, we can put the win ratio of the leading engine in the numerator and we get the same result. The win ratio is the sum of the wins and draws.

In R, there is a package called elo which we will also use here. But we can write our own functions for this purpose.

elo <- function(win_ratio) {400 * log10(win_ratio / (1-win_ratio))}

We can also check for the standard errors of ELO differences using a normal approximation.

denom95 <- function(win_ratio, total) qnorm(0.975) * sqrt(win_ratio * (1-win_ratio)/(total-1))

We can also compute for the LOS as described in the chessprogramming wiki site. I used three estimators here. LOS3 might become untenable with large data sets, but we only have 100 rows of data here so it will be fine.

LOS <- function(wins_losses, total) pnorm(total/2, sd = wins_losses)
LOS2 <- function(wins, losses) pnorm((wins-losses)/sqrt(wins+losses))
LOS3 <- function(wins, losses, draws) {
  total = wins + losses + draws
  exp = (wins/total)^wins * (losses/total)^losses * (draws/total)^draws
  factorials = factorial(total)/(factorial(wins)*factorial(losses)*factorial(draws))
  P = factorials * exp
  1-P
}

We will now extract the initials of the ECO codes, determine the points of Leela and SF after each game, the win rate (by the leading engine) after each game, the estimated ELO difference (elodiff) after each game, and the three LOS estimates after each game.

data <- data %>%
  mutate(ECO2 = substr(ECO1, start = 1, stop = 1)) %>%
  # calculate Leela's scores
  mutate(points.Leela = (White == "Leela") * points.White + (Black == "Leela") * points.Black) %>%
  # calculate SF's scores
  mutate(points.SF = (White == "SF") * points.White + (Black == "SF") * points.Black) %>%
  mutate(results.Leela = case_when(points.Leela == 1~"Win", 
                                   points.Leela == 0.5~"Draw",
                                   points.Leela == 0~"Loss")) %>%
  mutate(results.SF = case_when(points.SF == 1~"Win", 
                                   points.SF == 0.5~"Draw",
                                   points.SF == 0~"Loss")) %>%
  # calculate cumulative scores
  mutate(Score.Leela = cumsum(points.Leela)) %>%
  mutate(Score.SF = cumsum(points.SF)) %>%
  mutate(total = row_number()) %>%
  mutate(draw_ratio = cumsum(points.Leela == points.SF)/total) %>%
  mutate(wins.Leela = cumsum(results.Leela=="Win")) %>%
  mutate(losses.Leela = cumsum(results.Leela=="Loss")) %>%
  mutate(wins.SF = cumsum(results.SF=="Win")) %>%
  mutate(losses.SF = cumsum(results.SF=="Loss")) %>%
  mutate(Draws = cumsum(results.Leela=="Draw")) %>%
  # calculate win rate of Leela
  mutate(win_rate.Leela = Score.Leela/total) %>%
  mutate(elodiff = elo(win_rate.Leela)) %>%
  # calculate ELO's and LOS's
  mutate(SE = elo(win_rate.Leela + denom95(win_rate.Leela, total))-elodiff) %>%
  mutate(LOS = LOS(total*(1-draw_ratio), total)) %>%
  mutate(LOS2 = LOS2(wins.Leela, losses.Leela)) %>%
  mutate(LOS3 = LOS3(wins.Leela, losses.Leela, Draws)) 
data %>% 
  select(Opening, ECO2, win_rate.Leela:LOS3) %>% 
  flextable() %>% autofit()

Opening	ECO2	win_rate.Leela	elodiff	SE	LOS	LOS2	LOS3
1	E	0.50000	0.000	NaN	1.00000	NaN	0.00000
2	E	0.50000	0.000	NaN	1.00000	NaN	0.00000
3	B	0.50000	0.000	NaN	1.00000	NaN	0.00000
4	B	0.50000	0.000	NaN	1.00000	NaN	0.00000
5	A	0.50000	0.000	798.096	1.00000	NaN	0.00000
6	A	0.50000	0.000	472.706	1.00000	NaN	0.00000
7	C	0.50000	0.000	381.844	1.00000	NaN	0.00000
8	C	0.50000	0.000	330.843	1.00000	NaN	0.00000
9	A	0.50000	0.000	296.575	1.00000	NaN	0.00000
10	A	0.55000	34.860	303.216	1.00000	0.84134	0.61258
11	C	0.54545	31.672	275.265	1.00000	0.84134	0.61446
12	C	0.50000	0.000	235.953	0.99865	0.50000	0.85195
13	A	0.50000	0.000	222.815	0.99942	0.50000	0.85305
14	A	0.50000	0.000	211.674	0.99977	0.50000	0.85397
15	B	0.50000	0.000	202.066	0.99991	0.50000	0.85475
16	B	0.53125	21.743	201.982	0.99617	0.71815	0.88967
17	E	0.52941	20.461	193.375	0.99770	0.71815	0.89039
18	E	0.55556	38.764	193.252	0.98778	0.84134	0.90667
19	B	0.55263	36.708	185.531	0.99123	0.84134	0.90735
20	B	0.55000	34.860	178.692	0.99379	0.84134	0.90795
21	D	0.54762	33.190	172.577	0.99567	0.84134	0.90848
22	D	0.54545	31.672	167.066	0.99702	0.84134	0.90896
23	C	0.54348	30.288	162.064	0.99798	0.84134	0.90939
24	C	0.56250	43.658	161.609	0.99180	0.91014	0.91930
25	E	0.56000	41.894	157.009	0.99379	0.91014	0.91971
26	E	0.57692	53.879	156.601	0.98487	0.94876	0.92647
27	B	0.57407	51.854	152.357	0.98778	0.94876	0.92687
28	B	0.57143	49.975	148.453	0.99018	0.94876	0.92724
29	A	0.56897	48.230	144.845	0.99217	0.94876	0.92757
30	A	0.56667	46.602	141.496	0.99379	0.94876	0.92788
31	C	0.56452	45.082	138.377	0.99511	0.94876	0.92817
32	C	0.56250	43.658	135.463	0.99617	0.94876	0.92843
33	E	0.56061	42.321	132.731	0.99702	0.94876	0.92868
34	E	0.55882	41.065	130.163	0.99770	0.94876	0.92891
35	B	0.54286	29.853	125.947	0.99379	0.87158	0.94693
36	B	0.55556	38.764	125.458	0.98778	0.92135	0.95074
37	A	0.55405	37.708	123.295	0.98962	0.92135	0.95092
38	A	0.56579	45.982	122.853	0.98262	0.95221	0.95386
39	C	0.55128	35.760	119.293	0.97441	0.89705	0.96132
40	C	0.56250	43.658	118.857	0.96548	0.93417	0.96330
41	E	0.56098	42.582	117.004	0.96881	0.93417	0.96347
42	A	0.55952	41.558	115.239	0.97187	0.93417	0.96362
43	C	0.54651	32.413	112.361	0.96341	0.87589	0.96791
44	C	0.54545	31.672	110.813	0.96662	0.87589	0.96805
45	A	0.53333	23.197	108.340	0.95825	0.79731	0.97098
46	A	0.53261	22.691	106.965	0.96157	0.79731	0.97110
47	B	0.53191	22.207	105.642	0.96467	0.79731	0.97122
48	B	0.53125	21.743	104.367	0.96757	0.79731	0.97134
49	E	0.53061	21.298	103.139	0.97026	0.79731	0.97144
50	E	0.53000	20.871	101.953	0.97276	0.79731	0.97154
51	B	0.52941	20.461	100.808	0.97509	0.79731	0.97164
52	B	0.52885	20.067	99.701	0.97725	0.79731	0.97173
53	A	0.52830	19.687	98.631	0.97925	0.79731	0.97182
54	A	0.52778	19.322	97.595	0.98110	0.79731	0.97190
55	B	0.52727	18.970	96.591	0.98280	0.79731	0.97198
56	B	0.52679	18.630	95.618	0.98437	0.79731	0.97206
57	A	0.52632	18.303	94.675	0.98582	0.79731	0.97213
58	A	0.52586	17.987	93.759	0.98715	0.79731	0.97220
59	C	0.52542	17.681	92.869	0.98837	0.79731	0.97227
60	C	0.52500	17.386	92.005	0.98949	0.79731	0.97234
61	A	0.53279	22.815	91.660	0.98532	0.85748	0.97367
62	A	0.54032	28.080	91.333	0.98062	0.90165	0.97480
63	C	0.53968	27.632	90.503	0.98214	0.90165	0.97486
64	C	0.53906	27.199	89.695	0.98355	0.90165	0.97492
65	E	0.53846	26.779	88.909	0.98487	0.90165	0.97498
66	E	0.53788	26.371	88.144	0.98610	0.90165	0.97504
67	B	0.53731	25.976	87.398	0.98724	0.90165	0.97509
68	B	0.53676	25.593	86.672	0.98829	0.90165	0.97514
69	D	0.53623	25.221	85.964	0.98928	0.90165	0.97519
70	D	0.53571	24.859	85.273	0.99018	0.90165	0.97524
71	C	0.53521	24.508	84.598	0.99103	0.90165	0.97529
72	C	0.53472	24.166	83.940	0.99180	0.90165	0.97533
73	A	0.53425	23.834	83.297	0.99252	0.90165	0.97538
74	A	0.53378	23.511	82.669	0.99318	0.90165	0.97542
75	B	0.53333	23.197	82.055	0.99379	0.90165	0.97546
76	B	0.53289	22.891	81.455	0.99435	0.90165	0.97550
77	C	0.53247	22.593	80.868	0.99487	0.90165	0.97554
78	E	0.53205	22.302	80.294	0.99534	0.90165	0.97558
79	C	0.53165	22.019	79.732	0.99577	0.90165	0.97562
80	C	0.53125	21.743	79.182	0.99617	0.90165	0.97565
81	E	0.52469	17.171	78.364	0.99432	0.84134	0.97757
82	E	0.53049	21.211	78.116	0.99206	0.88737	0.97847
83	B	0.53012	20.955	77.599	0.99268	0.88737	0.97850
84	B	0.52976	20.705	77.092	0.99326	0.88737	0.97854
85	A	0.52941	20.461	76.595	0.99379	0.88737	0.97857
86	A	0.53488	24.279	76.365	0.99155	0.92135	0.97935
87	A	0.52874	19.990	75.630	0.98897	0.87433	0.98073
88	E	0.53409	23.726	75.405	0.98610	0.91014	0.98137
89	A	0.53371	23.458	74.939	0.98696	0.91014	0.98140
90	A	0.53333	23.197	74.481	0.98778	0.91014	0.98143
91	C	0.53297	22.941	74.032	0.98855	0.91014	0.98146
92	C	0.53261	22.691	73.591	0.98928	0.91014	0.98149
93	D	0.53226	22.446	73.158	0.98996	0.91014	0.98151
94	D	0.53723	25.921	72.954	0.98739	0.93668	0.98208
95	C	0.53684	25.647	72.531	0.98815	0.93668	0.98211
96	C	0.53646	25.379	72.115	0.98886	0.93668	0.98214
97	E	0.53608	25.116	71.706	0.98954	0.93668	0.98216
98	E	0.53571	24.859	71.305	0.99018	0.93668	0.98219
99	B	0.53535	24.607	70.910	0.99079	0.93668	0.98221
100	B	0.53500	24.360	70.522	0.99137	0.93668	0.98224

We see that by game 94, when Leela breached the 50.5 mark, the ELO difference is about 26, but with large error bar. The LOS’s show though that there is very high likelihood that Leela is indeed stronger. At the end of SuFi, the estimated ELO difference is about 24.

The problem with ELO estimates based on results of chess engine tournaments is that each opening has to be played in reverse colors by each engine. Also, there are families of ECO code openings. As such, the ELO differences might actually be biased. Also, the sample size of 100 is actually small, leading to the large error bars.

Instead, we can calculate the ELO differences by ECO family of openings. The estimates will have larger error bars because we now have smaller samples.

data2 <- data %>%
  group_by(ECO2) %>%
  mutate(ECO2.Score.Leela = cumsum(points.Leela)) %>%
  mutate(ECO2.Score.SF = cumsum(points.SF)) %>%
  mutate(ECO2.total = row_number()) %>%
  mutate(ECO2.draw_ratio = cumsum(points.Leela == points.SF)/ECO2.total) %>%
  mutate(ECO2.wins.Leela = cumsum(results.Leela=="Win")) %>%
  mutate(ECO2.losses.Leela = cumsum(results.Leela=="Loss")) %>%
  mutate(ECO2.wins.SF = cumsum(results.SF=="Win")) %>%
  mutate(ECO2.losses.SF = cumsum(results.SF=="Loss")) %>%
  mutate(ECO2.Draws = cumsum(results.Leela=="Draw")) %>%
  mutate(ECO2.win_rate.Leela = ECO2.Score.Leela/ECO2.total) %>%
  mutate(ECO2.elodiff = elo(ECO2.win_rate.Leela)) %>%
  mutate(ECO2.SE = elo(ECO2.win_rate.Leela + denom95(ECO2.win_rate.Leela, ECO2.total))-ECO2.elodiff) %>%
  mutate(ECO2.LOS = LOS(ECO2.total*(1-ECO2.draw_ratio), ECO2.total)) %>%
  mutate(ECO2.LOS2 = LOS2(wins.Leela, losses.Leela)) %>%
  mutate(ECO2.LOS3 = LOS3(wins.Leela, losses.Leela, Draws))

We can now see the estimated ELO differences at the last of game of each ECO group of openings.

data2 %>%
  slice(n()) %>% select(starts_with("ECO2")) %>% 
  select(1:8) %>%
  flextable() %>% autofit()

ECO2	ECO2.Score.Leela	ECO2.Score.SF	ECO2.total	ECO2.draw_ratio	ECO2.wins.Leela	ECO2.losses.Leela	ECO2.wins.SF
A	14.5	11.5	26	0.73077	5	2	2
B	12.5	11.5	24	0.87500	2	1	1
C	12.0	13.0	25	0.80000	2	3	3
D	3.5	2.5	6	0.83333	1	0	0
E	11.0	8.0	19	0.73684	4	1	1

data2 %>%
  slice(n()) %>% select(starts_with("ECO2")) %>% 
  select(9:16) %>%
  flextable() %>% autofit()

ECO2	ECO2.losses.SF	ECO2.Draws	ECO2.win_rate.Leela	ECO2.elodiff	ECO2.SE	ECO2.LOS	ECO2.LOS2	ECO2.LOS3
A	5	19	0.55769	40.268	152.79	0.96835	0.91014	0.98143
B	2	21	0.52083	14.485	153.91	0.99997	0.93668	0.98224
C	2	20	0.48000	-13.905	144.75	0.99379	0.93668	0.98214
D	1	5	0.58333	58.451	NaN	0.99865	0.93668	0.98208
E	4	14	0.57895	55.321	193.24	0.97128	0.93668	0.98219

Here it is very interesting to note that Leela actually performed relatively better in A and E openings. This is interesting because of the nature of the A and E openings. In particular, Jeroen said that E openings are too easy for the current top programs and he considered them very drawish.

We can instead use the elo package instead to calculate the ELO estimates. This package doesn’t have a function for estimating LOS though. The elomod object here is adjusted using a varying \(K\) after each round.

library(elo)
initial <- c(3589, 3587)
names(initial) <- c("Leela", "SF")
elomod <- elo.run(score(points.Leela, points.SF)~White+Black + regress(ECO2, initial, 0.2) + k(20*log(abs(points.Leela - points.SF) + 1)),data = data, initial.elos = initial)
summary(elomod)

## 
## An object of class 'elo.run.regressed', containing information on 2 teams and 100 matches, with 5 regressions.
## 
## Mean Square Error: 0.0506
## AUC: 0.9082
## Favored Teams vs. Actual Wins: 
##        Actual
## Favored  0 0.5  1
##   TRUE   1  36 13
##   (tie)  0   0  0
##   FALSE  6  43  1

elodf <- as.data.frame(elomod)
elodf$elodiff <- abs(elodf$elo.A - elodf$elo.B)
elodf$actual_score <- na.omit(data$Score.Leela)
elodf <- elodf %>%
  mutate(exp_score = cumsum(1 / (1+10^(elodiff/400))))
elodf %>% 
  mutate_if(is.numeric, function(x) round(x, 3)) %>%
  flextable() %>% autofit()

team.A	team.B	p.A	wins.A	update.A	update.B	elo.A	elo.B	elodiff	actual_score	exp_score
SF	Leela	0.497	0.5	0.000	0.000	3587.0	3589.0	2.000	0.5	0.497
Leela	SF	0.503	0.5	0.000	0.000	3589.0	3587.0	2.000	1.0	0.994
SF	Leela	0.497	0.5	0.000	0.000	3587.0	3589.0	2.000	1.5	1.491
Leela	SF	0.503	0.5	0.000	0.000	3589.0	3587.0	2.000	2.0	1.988
SF	Leela	0.497	0.5	0.000	0.000	3587.0	3589.0	2.000	2.5	2.486
Leela	SF	0.503	0.5	0.000	0.000	3589.0	3587.0	2.000	3.0	2.983
SF	Leela	0.497	0.5	0.000	0.000	3587.0	3589.0	2.000	3.5	3.480
Leela	SF	0.503	0.5	0.000	0.000	3589.0	3587.0	2.000	4.0	3.977
SF	Leela	0.497	0.5	0.000	0.000	3587.0	3589.0	2.000	4.5	4.474
Leela	SF	0.503	1.0	6.892	-6.892	3595.9	3580.1	15.783	5.5	4.951
SF	Leela	0.477	0.5	0.000	0.000	3580.1	3595.9	15.783	6.0	5.429
Leela	SF	0.523	0.0	-7.246	7.246	3588.6	3587.4	1.291	6.0	5.927
SF	Leela	0.498	0.5	0.000	0.000	3587.4	3588.6	1.291	6.5	6.425
Leela	SF	0.502	0.5	0.000	0.000	3588.6	3587.4	1.291	7.0	6.923
SF	Leela	0.498	0.5	0.000	0.000	3587.4	3588.6	1.291	7.5	7.421
Leela	SF	0.502	1.0	6.906	-6.906	3595.6	3580.4	15.102	8.5	7.900
SF	Leela	0.478	0.5	0.000	0.000	3580.4	3595.6	15.102	9.0	8.378
Leela	SF	0.522	1.0	6.630	-6.630	3602.2	3573.8	28.363	10.0	8.837
SF	Leela	0.459	0.5	0.000	0.000	3573.8	3602.2	28.363	10.5	9.296
Leela	SF	0.541	0.5	0.000	0.000	3602.2	3573.8	28.363	11.0	9.756
SF	Leela	0.459	0.5	0.000	0.000	3573.8	3602.2	28.363	11.5	10.215
Leela	SF	0.541	0.5	0.000	0.000	3602.2	3573.8	28.363	12.0	10.674
SF	Leela	0.459	0.5	0.000	0.000	3573.8	3602.2	28.363	12.5	11.133
Leela	SF	0.541	1.0	6.367	-6.367	3608.5	3567.5	41.097	13.5	11.575
SF	Leela	0.441	0.5	0.000	0.000	3567.5	3608.5	41.097	14.0	12.016
Leela	SF	0.559	1.0	6.115	-6.115	3614.7	3561.3	53.328	15.0	12.440
SF	Leela	0.424	0.5	0.000	0.000	3561.3	3614.7	53.328	15.5	12.863
Leela	SF	0.576	0.5	0.000	0.000	3614.7	3561.3	53.328	16.0	13.287
SF	Leela	0.424	0.5	0.000	0.000	3561.3	3614.7	53.328	16.5	13.711
Leela	SF	0.576	0.5	0.000	0.000	3614.7	3561.3	53.328	17.0	14.135
SF	Leela	0.424	0.5	0.000	0.000	3561.3	3614.7	53.328	17.5	14.559
Leela	SF	0.576	0.5	0.000	0.000	3614.7	3561.3	53.328	18.0	14.983
SF	Leela	0.424	0.5	0.000	0.000	3561.3	3614.7	53.328	18.5	15.407
Leela	SF	0.576	0.5	0.000	0.000	3614.7	3561.3	53.328	19.0	15.830
SF	Leela	0.424	0.0	-5.876	5.876	3555.5	3620.5	65.079	19.0	16.238
Leela	SF	0.593	1.0	5.648	-5.648	3626.2	3549.8	76.375	20.0	16.630
SF	Leela	0.392	0.5	0.000	0.000	3549.8	3626.2	76.375	20.5	17.021
Leela	SF	0.608	1.0	5.432	-5.432	3631.6	3544.4	87.239	21.5	17.398
SF	Leela	0.377	0.0	-5.227	5.227	3539.2	3636.8	97.692	21.5	17.761
Leela	SF	0.637	1.0	5.032	-5.032	3641.9	3534.1	107.757	22.5	18.111
SF	Leela	0.350	0.5	0.000	0.000	3534.1	3641.9	107.757	23.0	18.461
Leela	SF	0.650	0.5	0.000	0.000	3641.9	3534.1	107.757	23.5	18.811
SF	Leela	0.350	0.0	-4.848	4.848	3529.3	3646.7	117.453	23.5	19.148
Leela	SF	0.663	0.5	0.000	0.000	3646.7	3529.3	117.453	24.0	19.485
SF	Leela	0.337	0.0	-4.674	4.674	3524.6	3651.4	126.800	24.0	19.810
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	24.5	20.135
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	25.0	20.461
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	25.5	20.786
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	26.0	21.111
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	26.5	21.436
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	27.0	21.761
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	27.5	22.087
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	28.0	22.412
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	28.5	22.737
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	29.0	23.062
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	29.5	23.387
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	30.0	23.713
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	30.5	24.038
SF	Leela	0.325	0.5	0.000	0.000	3524.6	3651.4	126.800	31.0	24.363
Leela	SF	0.675	0.5	0.000	0.000	3651.4	3524.6	126.800	31.5	24.688
SF	Leela	0.325	1.0	9.355	-9.355	3534.0	3642.0	108.091	32.5	25.038
Leela	SF	0.651	1.0	4.842	-4.842	3646.9	3529.1	117.775	33.5	25.374
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	34.0	25.711
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	34.5	26.048
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	35.0	26.384
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	35.5	26.721
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	36.0	27.058
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	36.5	27.395
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	37.0	27.731
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	37.5	28.068
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	38.0	28.405
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	38.5	28.741
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	39.0	29.078
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	39.5	29.415
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	40.0	29.752
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	40.5	30.088
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	41.0	30.425
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	41.5	30.762
SF	Leela	0.337	0.5	0.000	0.000	3529.1	3646.9	117.775	42.0	31.098
Leela	SF	0.663	0.5	0.000	0.000	3646.9	3529.1	117.775	42.5	31.435
SF	Leela	0.337	0.0	-4.668	4.668	3524.4	3651.6	127.111	42.5	31.760
Leela	SF	0.675	1.0	4.503	-4.503	3656.1	3519.9	136.117	43.5	32.074
SF	Leela	0.314	0.5	0.000	0.000	3519.9	3656.1	136.117	44.0	32.387
Leela	SF	0.686	0.5	0.000	0.000	3656.1	3519.9	136.117	44.5	32.701
SF	Leela	0.314	0.5	0.000	0.000	3519.9	3656.1	136.117	45.0	33.014
Leela	SF	0.686	1.0	4.347	-4.347	3660.4	3515.6	144.810	46.0	33.317
SF	Leela	0.303	0.0	-4.199	4.199	3511.4	3664.6	153.208	46.0	33.610
Leela	SF	0.707	1.0	4.059	-4.059	3668.7	3507.3	161.326	47.0	33.893
SF	Leela	0.283	0.5	0.000	0.000	3507.3	3668.7	161.326	47.5	34.176
Leela	SF	0.717	0.5	0.000	0.000	3668.7	3507.3	161.326	48.0	34.459
SF	Leela	0.322	0.5	0.000	0.000	3523.3	3652.7	129.461	48.5	34.781
Leela	SF	0.678	0.5	0.000	0.000	3652.7	3523.3	129.461	49.0	35.103
SF	Leela	0.322	0.5	0.000	0.000	3523.3	3652.7	129.461	49.5	35.425
Leela	SF	0.678	1.0	4.462	-4.462	3657.2	3518.8	138.384	50.5	35.736
SF	Leela	0.345	0.5	0.000	0.000	3532.4	3643.6	111.108	51.0	36.081
Leela	SF	0.655	0.5	0.000	0.000	3643.6	3532.4	111.108	51.5	36.426
SF	Leela	0.374	0.5	0.000	0.000	3543.4	3632.6	89.286	52.0	36.801
Leela	SF	0.626	0.5	0.000	0.000	3632.6	3543.4	89.286	52.5	37.175
SF	Leela	0.398	0.5	0.000	0.000	3552.1	3623.9	71.829	53.0	37.573
Leela	SF	0.602	0.5	0.000	0.000	3623.9	3552.1	71.829	53.5	37.971

Let us now investigate the evals.

data_df <- data %>% gather(color, engine, White:Black)

data_dfwhite <- data_df %>%
  filter(color == "White") %>%
  group_by(engine) %>%
  gather(evalengines, evals, Leela.openeval:SF.openeval) %>%
  mutate(evalengines = str_remove(evalengines, ".openeval")) %>%
  group_by(ECO2, evalengines) %>%
  summarize(mean = round(mean(evals),3), sd = round(sd(evals),3))
data_dfwhite %>% flextable() %>% autofit()

ECO2	evalengines	mean	sd
A	Leela	1.033	0.288
A	SF	0.614	0.282
B	Leela	0.807	0.586
B	SF	0.456	0.464
C	Leela	0.192	0.917
C	SF	0.106	0.605
D	Leela	0.735	0.191
D	SF	0.358	0.300
E	Leela	0.878	0.274
E	SF	0.633	0.366

data_df %>%
  filter(color == "White") %>%
  group_by(engine) %>%
  gather(evalengines, evals, Leela.openeval:SF.openeval) %>%
  mutate(evalengines = str_remove(evalengines, ".openeval")) %>%
  ggplot(aes(evals, color = evalengines)) + 
  geom_density() +
  facet_wrap(~ECO2+engine)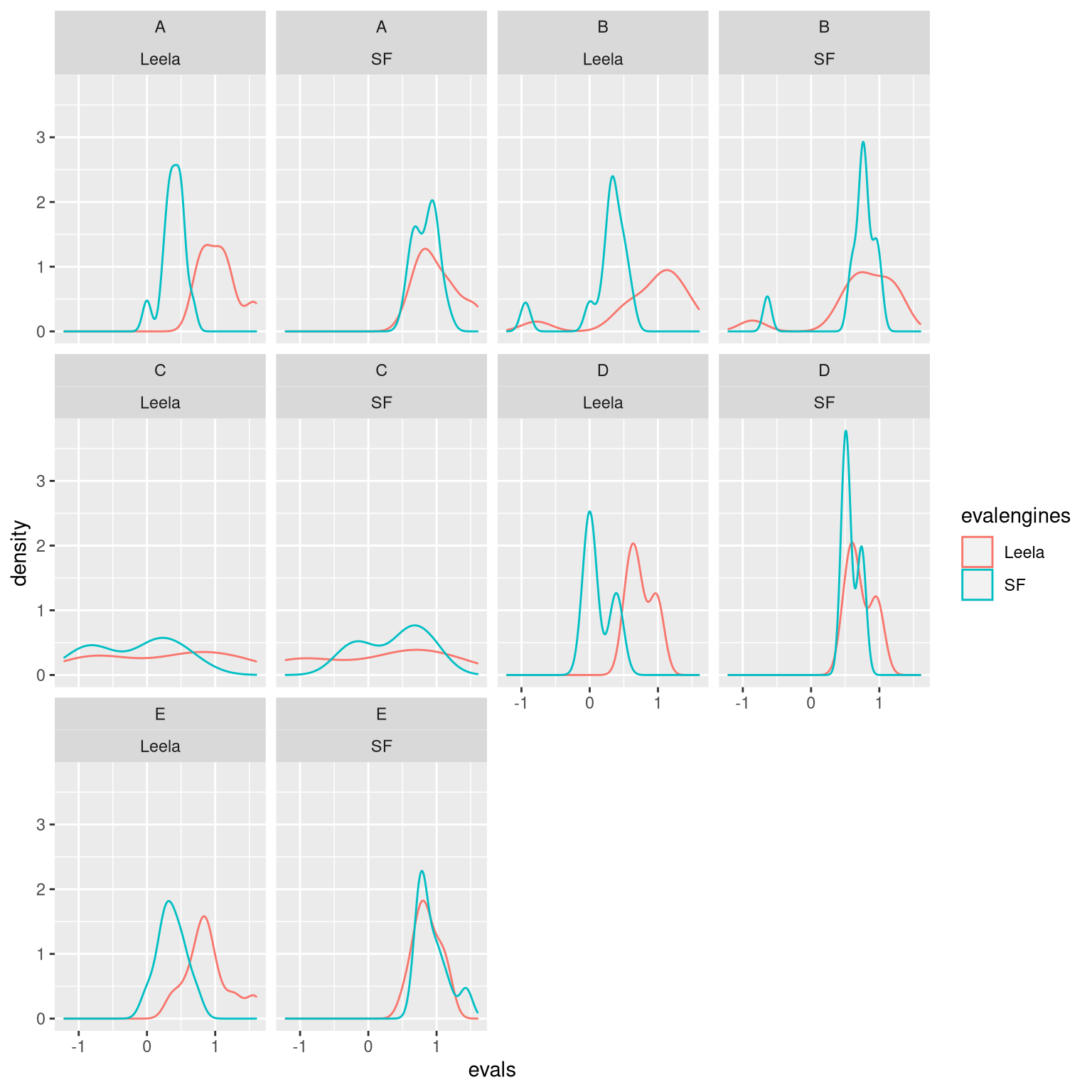

data_dfblack <- data_df %>%
  filter(color == "Black") %>%
  group_by(engine) %>%
  gather(evalengines, evals, Leela.openeval:SF.openeval) %>%
  mutate(evalengines = str_remove(evalengines, ".openeval")) %>%
  group_by(ECO2, evalengines) %>%
  summarize(mean = round(mean(evals),3), sd = round(sd(evals),3))
data_dfblack %>% flextable() %>% autofit()

ECO2	evalengines	mean	sd
A	Leela	1.033	0.288
A	SF	0.614	0.282
B	Leela	0.807	0.586
B	SF	0.456	0.464
C	Leela	0.192	0.917
C	SF	0.106	0.605
D	Leela	0.735	0.191
D	SF	0.358	0.300
E	Leela	0.878	0.274
E	SF	0.633	0.366

data_df %>%
  filter(color == "Black") %>%
  group_by(engine) %>%
  gather(evalengines, evals, Leela.openeval:SF.openeval) %>%
  mutate(evalengines = str_remove(evalengines, ".openeval")) %>%
  ggplot(aes(evals, color = evalengines)) + 
  geom_density() +
  facet_wrap(~ECO2+engine)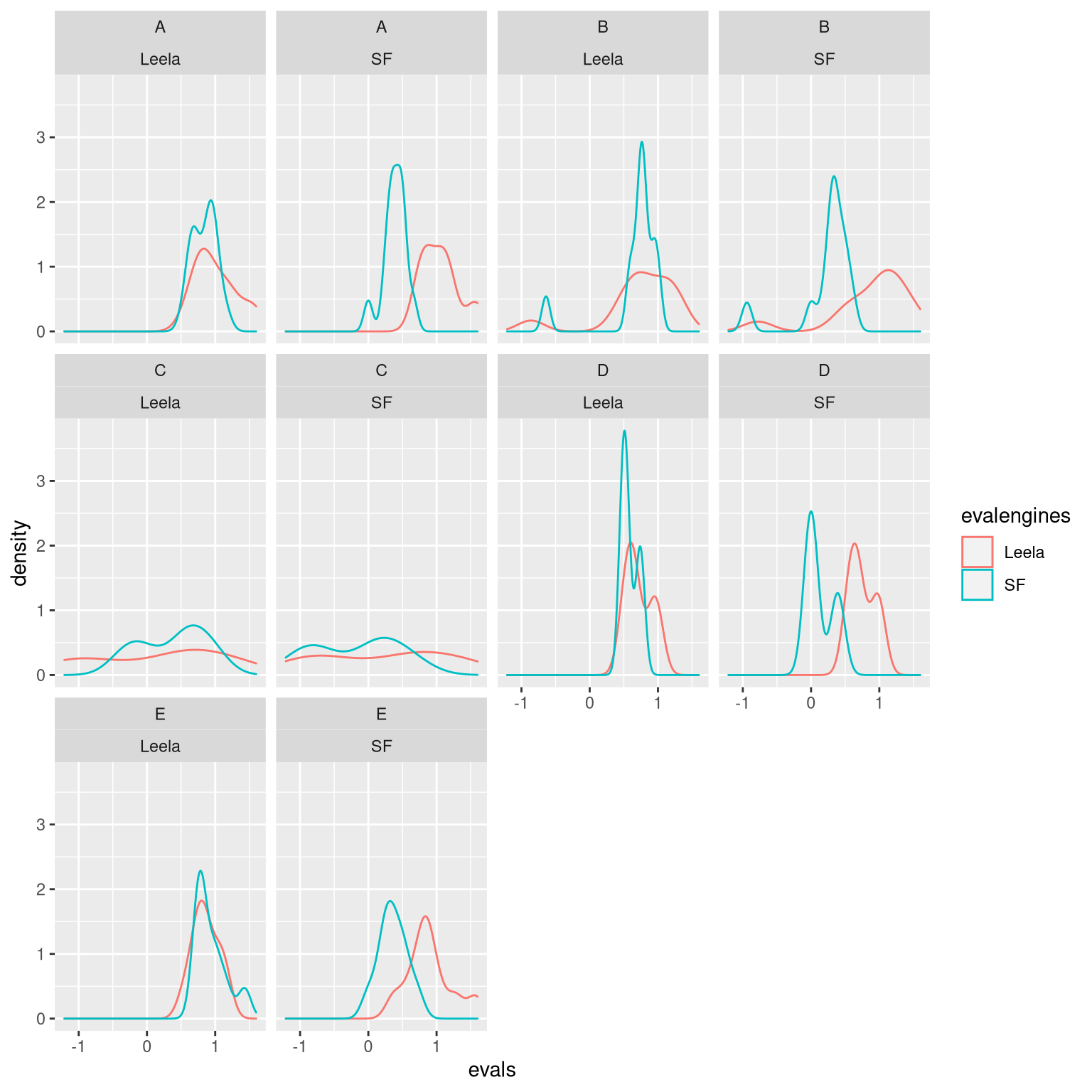

We can see that Leela’s opening evals are generally more optimistic than that of Stockfish, which can be attributed partly to SF’s contempt. But a closer inspection of Leela’s evals, we see that they are consistent even if playing as different colors. Leela also tends to win in openings where its opening evals are visibly more optimistic than that of Stockfish, signifying that Leela has better opening evaluation.

This has been a very exciting SuFi. I had a lot of fun engaging in many interesting and lively discussions in chat, although oftentimes the chat can quickly turn cancerous.

To end this post, I would like to congratulate the Leela devs and community for winning their first ever SuFi title. Kudos also to the SF team for continuing to improve a chess monster. I hope that Leela and SF continue to expose each other’s weaknesses, and get better as a result. Exciting times for the chess engine fans!